
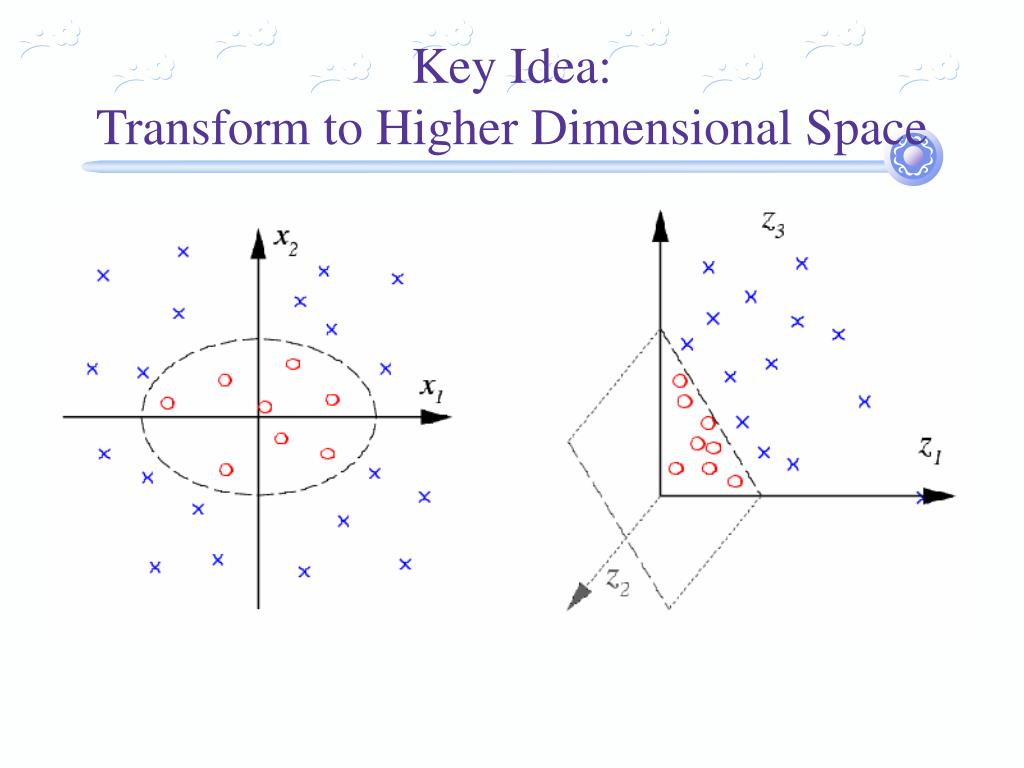
High Dimensionality: SVM is an effective tool in high-dimensional spaces, which is particularly applicable to document classification and sentiment analysis where the dimensionality can be extremely large. Let us now look at some advantages and disadvantages of SVM: Simply, these kernels transform our data to pass a linear hyperplane and thus classify our data. Common types of kernels used to separate non-linear data are polynomial kernels, radial basis kernels, and linear kernels (which are the same as support vector classifiers). This is known as the kernel trick, which enlarges the feature space in order to accommodate a non-linear boundary between the classes. Tell SVM to do its thing, but using the new dot product - we call this a kernel function.Figure out what the dot product in that space looks like:.This means that we can sidestep the expensive calculations of the new dimensions! This is what we do instead: Here’s a trick: SVM doesn’t need the actual vectors to work its magic, it actually can get by only with the dot products between them. Doing this for every vector in the dataset can be a lot of work, so it’d be great if we could find a cheaper solution. However, it turns out that calculating this transformation can get pretty computationally expensive: there can be a lot of new dimensions, each one of them possibly involving a complicated calculation. In the above example, we found a way to classify nonlinear data by cleverly mapping our space to a higher dimension. What’s left is mapping it back to two dimensions:Īnd there we go! Our decision boundary is a circumference of radius 1, which separates both tags using SVM.

That’s great! Note that since we are in three dimensions now, the hyperplane is a plane parallel to the $x$ axis at a certain $z$ (let’s say $z = 1$). Taking a slice of that space, it looks like this: This will give us a three-dimensional space. We create a new z dimension, and we rule that it be calculated a certain way that is convenient for us: $z = x² + y²$ (you’ll notice that’s the equation for a circle). Up until now, we had two dimensions: $x$ and $y$. So here’s what we’ll do: we will add a third dimension. However, the vectors are very clearly segregated, and it looks as though it should be easy to separate them. It’s pretty clear that there’s not a linear decision boundary (a single straight line that separates both tags). Sadly, usually things aren’t that simple. Now the example above was easy since clearly, the data was linearly separable - we could draw a straight line to separate red and blue. In other words: the hyperplane (remember it’s a line in this case) whose distance to the nearest element of each tag is the largest. This line is the decision boundary: anything that falls to one side of it we will classify as blue, and anything that falls to the other as red.īut, what exactly is the best hyperplane? For SVM, it’s the one that maximizes the margins from both tags. We plot our already labeled training data on a plane:Ī support vector machine takes these data points and outputs the hyperplane (which in two dimensions it’s simply a line) that best separates the tags. We want a classifier that, given a pair of (x,y) coordinates, outputs if it’s either red or blue. Let’s imagine we have two tags: red and blue, and our data has two features: x and y. The basics of Support Vector Machines and how it works are best understood with a simple example. Support Vector Machines Algorithm Linear Data What that essentially means is we will skip as much of the math as possible and develop a strong intuition of the working principle. I’ll focus on developing intuition rather than rigor. In this tutorial, we will try to gain a high-level understanding of how SVMs work and then implement them using R. However, they are mostly used in classification problems. In machine learning, support vector machines are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis.


 0 kommentar(er)
0 kommentar(er)
